8.1. The exact equation

The linear advection equation (eq. (8.5)) is given by:

\[\frac{\partial u}{\partial t} + a \frac{\partial u}{\partial x} = 0, a>0\]

We will assume an initial condition in the form of a simple wave:

(8.6)\[ u(x,0)=A e^{i k x},\]

where \(k = 2\pi/\lambda\) is the wave number (\(\lambda\) is the wavelength).

8.1.1. The analytical solution

We can find the analytic (exact) solution of (8.5) using the method separation of variables. Let the solution to (8.5) with initial condition (8.6) be given by:

(8.7)\[u(x,t)=G(t)H(x)\]

We substitute \(u(x,t)=G(t)H(x)\) in (8.5), and separate the x- and t-dependent terms on wither side of the equal sign:

\[\begin{split}\begin{aligned} \frac{\partial }{\partial t} (G(t)H(x))=& -a \frac{\partial }{\partial x} (G(t)H(x)) \\ H(x)\frac{\partial G(t)}{\partial t} =& -a G(t) \frac{\partial H(x)}{\partial x} \\ \frac{1}{G(t)} \frac{\partial G(t)}{\partial t} =& -a \frac{1}{H(x)} \frac{\partial H(x)}{\partial x}, \end{aligned}\end{split}\]

The equal sign can only hold for all \((x,t)\) if both side are equal to a constant value, \(-\alpha\). We can now integrate each side of the equation, yielding

\[\begin{split}\begin{aligned} \frac{1}{G(t)} \frac{\partial G(t)}{\partial t} =& -\alpha \Leftrightarrow G(t)=A_1e^{-\alpha t} \\ -a \frac{1}{H(x)} \frac{\partial H(x)}{\partial x}=& -\alpha \Leftrightarrow H(x)=A_2e^{\alpha x/a}, \end{aligned}\end{split}\]

We can now subsitute the expressions for \(G(t)\) and \(H(x)\) into (8.7) and find \(u(x,t)=G(t)H(x)=A_1A_2e^{-\alpha t}e^{\alpha x/a}\).

Using the initial conditions (8.5) at \(t=0\) we have \(u(x,0)=A_1A_2e^{\alpha x/c}\), so we know that \(A=A_1A_2\) and \(ik = \alpha/a\) and so \(\alpha=ika\). Finally, we can write:

(8.8)\[ u(x,t)=Ae^{-ikct}e^{ikcx/c}=Ae^{ik(x-at)},\]

which is the solution of (8.5) given the initial condition (8.6). This solution represents the initial condition moving along the positive \(x\)-direction with translation velocity \(a\).

For a general case, where an initial condition \(u(t=0,x)=u_0\) is known, the solution to the linear advection equation becomes:

(8.9)\[u(t,x)=u_0(x-at)\]

8.1.2. Characteristics of the linear advection equation

The analytical solution to the linear advection equation (eq (8.5)) is given by \(u(x,t)=u_0(x-at)\), or we can write it as \(u(x-at,0)\). For this to be true, the solution must be constant along the charachteristics \(x-at\). We can sketch this in the \(x-t\) space:

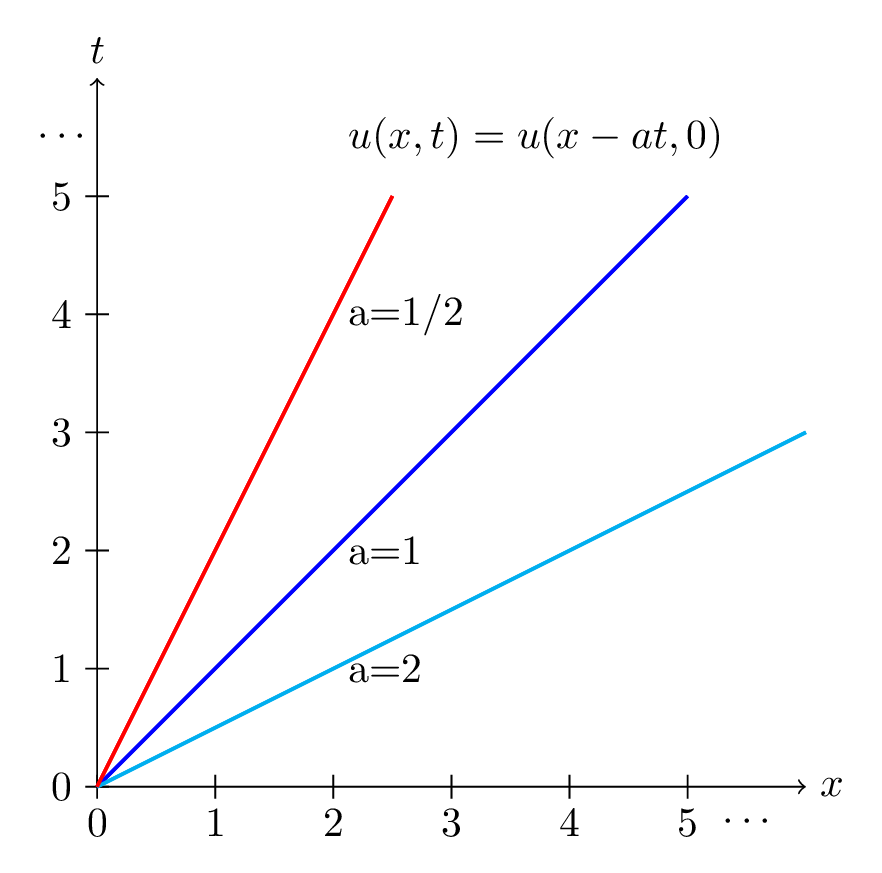
Fig. 8.1 The charactheristics for linear advection with different values of \(a\) in different colors. The solution starting at any of these characteristics will stay at the charachteristics as they translate in time and space.

Alternatively, we can translate the charactheristics to find how they look while passing through the grid point \((m,n)\). The domain of dependence for the exact solution, will lie along the charachteristics.

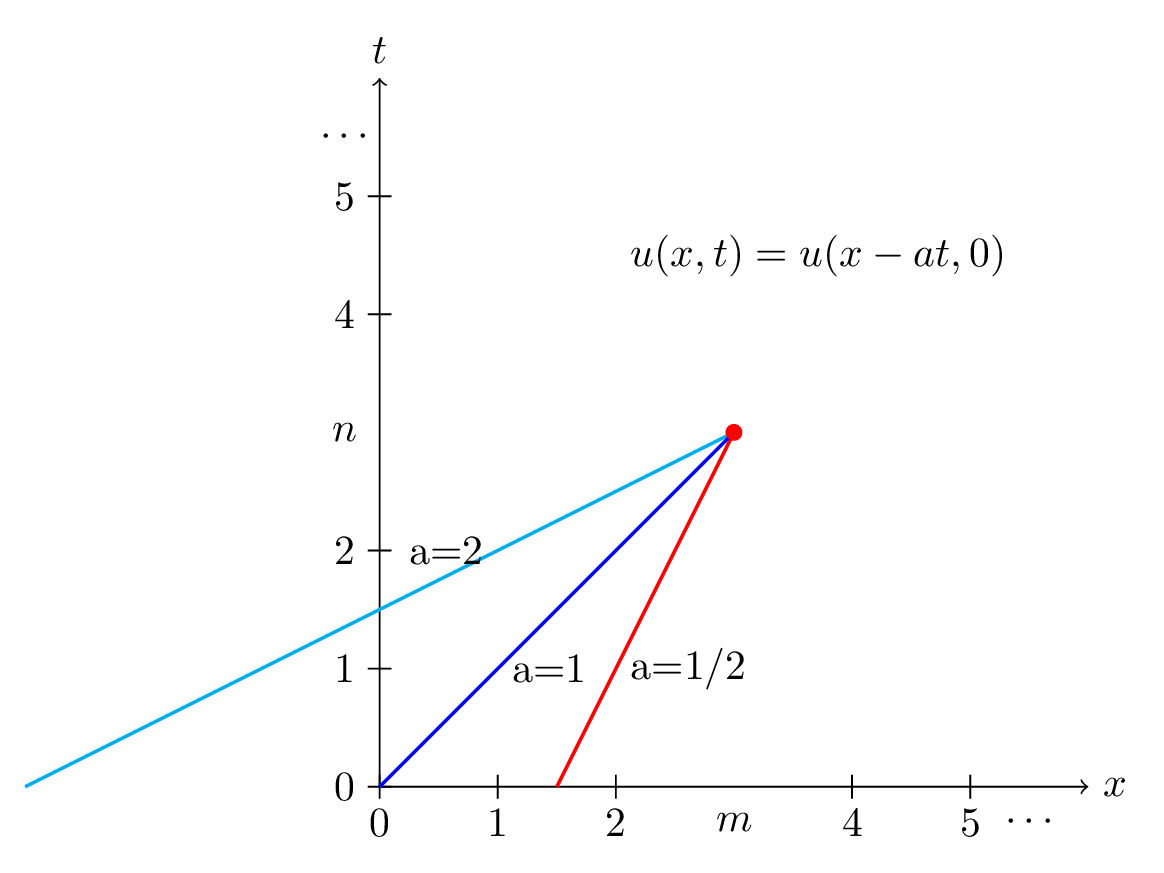
Fig. 8.2 The charactheristics for linear advection with different values of \(a\) in different colors. The solution starting at any of these characteristics will stay at the charachteristics as they translate in time and space.