4.3. Courant-Friedrich-Lewy, CFL criterion

The CFL criterion is named after the mathematicians Richard Courant, Kurt Otto Friederichs and Hans Lewy who published a piece “On the partial difference equations of mathematical physics” in 1928, where they discuss the factor and how it relates to stability.

To understand where the CFL criterion comes from, we can, for example, look at the FTBS scheme for the linear advection equation:

\[q_m^{n+1}=q_m^n-a\frac{\Delta t}{\Delta x}(q_m^n-q_{m-1}^n)\]

Definition

The factor \(C=a\frac{\Delta t}{\Delta x}\) is typically called the Courant number

CFL criterion

\(C=a\frac{\Delta t}{\Delta x}\leq C_{max}\) is the CFL criterion for stability of the one-dimensional linear advection equation.

When examining the CFL number, we compare the size of the displacement during one time step (\(a\Delta t\)) to the grid cell size \(\Delta x\). For most numerical schemes, \(C\leq 1\) is a necessary (but not sufficient!) condition for stability. If the displacement is much larger than the grid cell size, \(C>>1\), the signal travels many grid cells in just one time step. This means that we cannot calculate the next time step based on the few neighboring grid points like we do in the simple Finite Difference schemes.

For the two-dimensional non-linear advection equation,

\[\frac{\partial q}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y},\]

the CFL criterion looks similar:

definition:CFL)=

CFL criterion in 2D

\(C=u\frac{\Delta t}{\Delta x}+v\frac{\Delta t}{\Delta y}\leq C_{max}\) is the CFL criterion for stability of the two-dimensional non-linear advection equation.

4.3.1. Characteristics of the linear advection equation vs Domain of dependence

We can combine the figures showing the numerical domain of dependence for the FTBS scheme (Fig. 4.1) and the exact domain of dependence from the charactheristics of the advection equation (Fig. 8.2), we obtain:

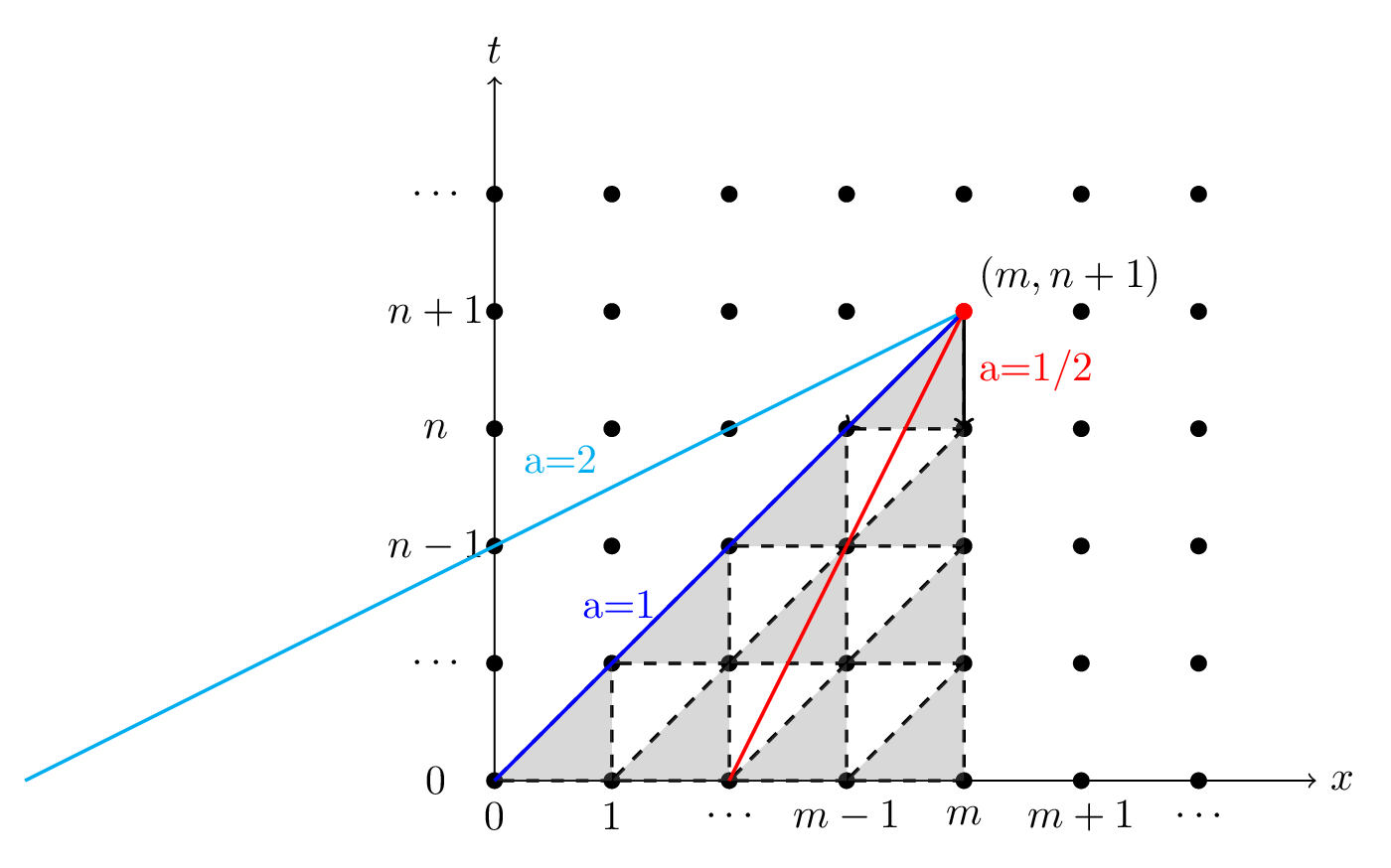
Fig. 4.2 name: fig:Char3 Domain of dependence for the exact (analytical) solution of the linear advection equation (colors) and for the FTBS scheme (shaded triangles).

If the analytical domain of dependence lies within the numerical domain of dependence of a given scheme, then the scheme fullfills a necessary (but not sufficient) requirement for stability.

The slope of the charachteristic (i.e., physical DoD) is \(1/a\). The slope of the nuemrical DoD is \(\Delta t/\Delta x\). The physical DoD is within the numerical DoD if \(\frac{\Delta t}{\Delta x}\leq \frac{1}{a}\).

This is true if \(a\frac{\Delta t}{\Delta x}\leq 1\). We recognize this as the CFL conditions, where \(C=a\frac{\Delta t}{\Delta x}\)