8.2. The difference equation

We are going to solve equation (8.5) numerically on discretized time and space. The discretizations are:

(8.10)\[\begin{split} x_m &= m\Delta x, m=0,1,2,...,M \\ t^n &= n\Delta t, n=0,1,2,...,N,\end{split}\]

where \(\Delta t\) is the time step and \(\Delta x\) is the grid resolution. The discrete time-space domain is commonly represented as the t-x diagram in Fig. 8.3.

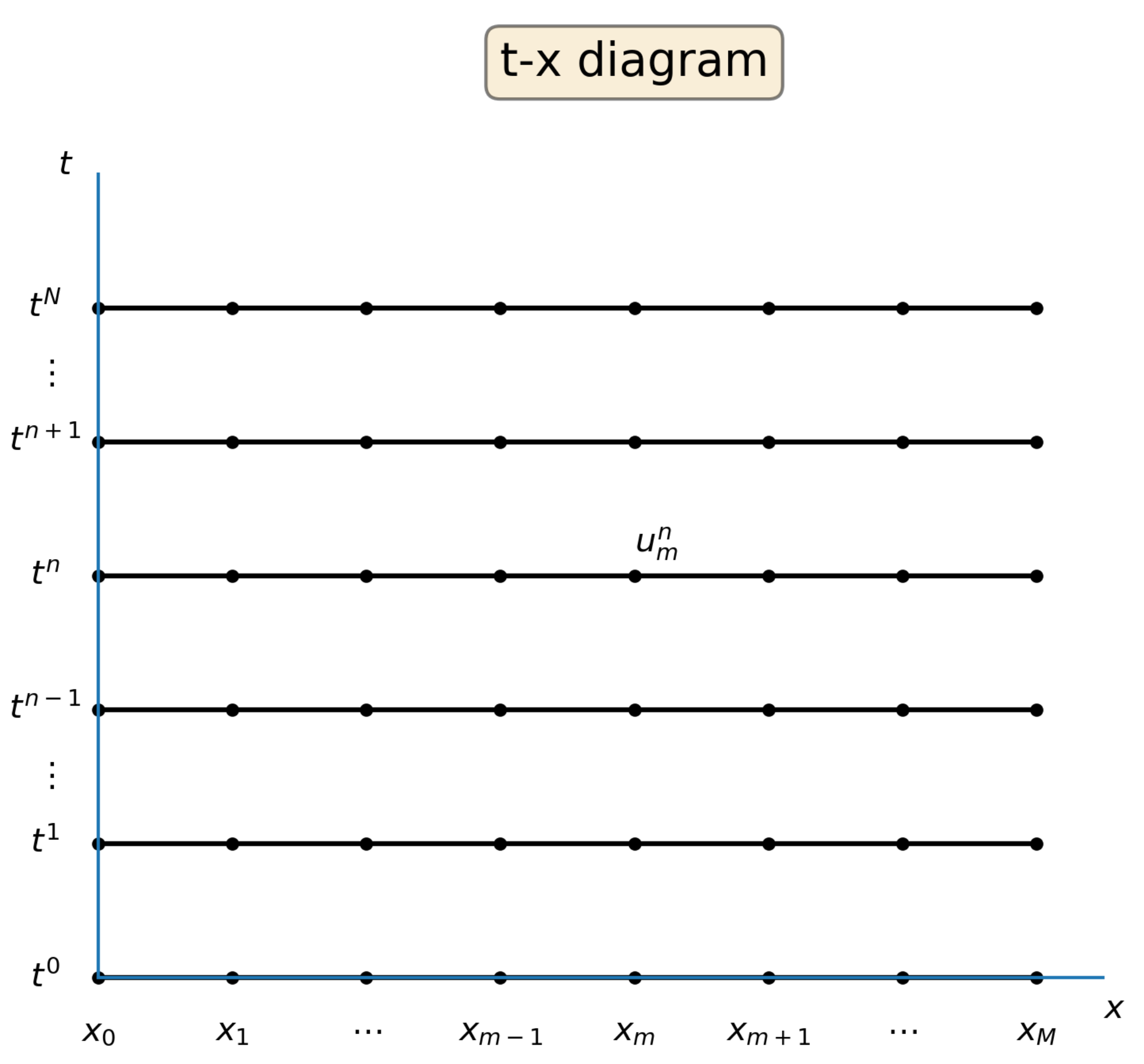
Fig. 8.3 The discrete time-space domain represented as a t-x diagram. The numerical solution at time \(t^n\) and position \(x_m\) is \(u_m^n\) and is represented in the diagram in the position (\(x_m\),\(t^n\)).

Using the 2nd order centered formula (3.17) to replace the exact derivatives in (8.5), we get a Centered in Time, Centered in Space (CTCS) scheme:

(8.11)\[ \frac{u_{m}^{n+1} - u_{m}^{n-1}}{2\Delta t } + c \frac{u_{m+1}^{n} - u_{m-1}^{n}}{2\Delta x} = 0.\]

We call (8.11) the difference equation resulting from the discretization of (8.5) by the 2nd order centred formulas for the first derivative. Rearranging the terms of (8.11) we obtain a time marching scheme:

(8.12)\[u_{m}^{n+1} = u_{m}^{n-1} - c\frac{\Delta t}{\Delta x}(u_{m+1}^{n}-u_{m-1}^{n}),\]

The CTCS scheme is also known as the leapfrog scheme, which is a three-level scheme, because it employs information at time levels \(n-1\), \(n\) and \(n+1\). Since the discretization of (8.5) was done with 2nd order formulas, the scheme (8.12) is of 2nd order.

Similarly, we can obtain schems with other combination of formulas for the space and time derivative. The Forward in Tie, Backward in space (FTBS) scheme would look like:

(8.13)\[u_m^{n+1}=u_m^n-\frac{a\Delta t}{\Delta x}(u_{m+1}^n-u_m^n)\]