3.4. Finite difference formulas for the 1st derivative

3.4.1. First order formulas

Finite difference formulas are just finite difference approximations, disregarding the truncation error. We can use Taylor series expansions to obtain several lower order finite difference formulas.

We typically start from equation (3.4), repeated here:

\[u(t)=u^n+\frac{u'(t^n)}{1!}(t-t^n)+\frac{u''(t^n)}{2!}(t-t^n)^2+\sum_{p=3}^{\infty}\frac{u^{(p)}(t^n)}{p!}(t-t^n)^p\]

3.4.1.1. Forward difference formula

From (3.6), we have

(3.12)\[\frac{du}{dt}=\frac{u^{n+1}-u^n}{\Delta t}+O(\Delta t).\]

Formula (3.12) is called a forward difference formula because it uses the \(u^n\) and the \(u^{n+1}\) values, and it is a first order formula because the truncation error is of \(O(\Delta t)\). The leading term of the truncation error is usually written with the formula to indicate its order of approximation.

3.4.1.2. Backward difference formula

To achieve a backward Taylor series, we let \(t=t^{n-1}\) and insert into (3.4):

(3.13)\[u^{n-1}=u^n+(t^{n-1}-t^{n})\frac{du}{dt}|_{t^n}+\frac{(t^{n-1}-t^{n})}{2!}\frac{d^2u}{dt^2}|_{t^n}+\sum_{p=3}^{\infty}\frac{(t^{n-1}-t^{n})^p}{p!}\frac{d^{(p)}u}{dt^p}|_{t^n}\]

We note that \(t^{n-1}-t^{n}=-\Delta t\) and replace these terms:

(3.14)\[u^{n-1}=u^n+(-\Delta t)\frac{du}{dt}|_{t^n}+\frac{(-\Delta t)^2}{2!}\frac{d^2u}{dt^2}|_{t^n}+\sum_{p=3}^{\infty}\frac{(-\Delta t)^p}{p!}\frac{d^{(p)}u}{dt^p}|_{t^n}\]

We can now adjust the signs from \(\Delta t\) to get:

(3.15)\[ u^{n-1}=u^n-\Delta t\frac{du}{dt}|_{t^n}+\frac{(\Delta t)^2}{2!}\frac{d^2u}{dt^2}|_{t^n}+\sum_{p=3}^{\infty}\frac{(-\Delta t)^p}{p!}\frac{d^{(p)}u}{dt^p}|_{t^n} \]

We finally rearrange the terms to isolate \(\frac{du}{dt}\) and obtain the backward difference formula for the 1st derivative:

(3.16)\[\frac{du}{dt}=\frac{u^{n}-u^{n-1}}{\Delta t} + O\left( \Delta t\right),\]

which uses the \(u^{n-1}\) and the \(u^{n}\) values and is also a first order approximation.

3.4.1.3. Centered difference formula

We can combine the forward and backward difference formulas to achieve a centered formula. we can, for example sum the forward (eq. (3.12)) and backward (eq. (3.16)) Taylor expansions and dividing by 2, to obtain the simplest centered difference formula:

(3.17)\[\frac{du}{dt}=\frac{u^{n+1}-u^{n-1}}{2\Delta t} + O\left( \Delta t^2\right),\]

Since the backward and forward Taylor expansions have opposite signs for every second term, these terms cancel out. We, therefore, cancel out the first error term, and now have a second order approximation, with a truncation error proportional to \(\Delta t^2\).

3.4.2. Higher order formulas

The 1st and 2nd order formulas (3.12), (3.16), (3.17) were obtained by manipulation of the Taylor series expansions of \(u(t)\) but for higher order approximations, this soon becomes unpractical. However, there is a more expedite method to find higher order formulas.

As the 2nd order formula needed more information about \(u\) than the 1st order formulas, i.e. it needed more data points, we expect that higher order formulas will require even more data points. Let us consider the values of \(u\) at \(n-2\), \(n-1\), \(n\), \(n+1\), \(n+2\), and form an expression for the time derivative using the function values at these time steps:

\[\left.\frac{du}{dt}\right|_{t^n} \approx a_{-2}u^{n-2}+a_{-1}u^{n-1}+a_{0}u^{n}+a_{1}u^{n+1}+a_{2}u^{n+2}, \]

where the \(a_j\)’s are coefficients to be determined.

We start by expanding \(u^{j}, \quad j=n-2,\dotsc,n+2\) as Taylor series of \(u^n\), up to the fifth order term:

\[\begin{split}\begin{aligned} u^{n-2} &= u^n - 2\Delta t\frac{du}{dt}+4\frac{\Delta t^2}{2}\frac{d^2u}{dt^2}-8\frac{\Delta t^3}{6}\frac{d^3u}{dt^3}+16\frac{\Delta t^4}{24}\frac{d^4u}{dt^4}-32\frac{\Delta t^5}{120}\frac{d^5u}{dt^5} + O(\Delta t^6)\\ u^{n-1} &= u^n - \Delta t\frac{du}{dt}+\frac{\Delta t^2}{2}\frac{d^2u}{dt^2}-\frac{\Delta t^3}{6}\frac{d^3u}{dt^3}+\frac{\Delta t^4}{24}\frac{d^4u}{dt^4}-\frac{\Delta t^5}{120}\frac{d^5u}{dt^5} + O(\Delta t^6)\\ u^{n} &= u^n \\ u^{n+1} &= u^n + \Delta t\frac{du}{dt}+\frac{\Delta t^2}{2}\frac{d^2u}{dt^2}+\frac{\Delta t^3}{6}\frac{d^3u}{dt^3}+\frac{\Delta t^4}{24}\frac{d^4u}{dt^4}+\frac{\Delta t^5}{120}\frac{d^5u}{dt^5} + O(\Delta t^6)\\ u^{n+2} &= u^n + 2\Delta t\frac{du}{dt}+4\frac{\Delta t^2}{2}\frac{d^2u}{dt^2}+8\frac{\Delta t^3}{6}\frac{d^3u}{dt^3}+16\frac{\Delta t^4}{24}\frac{d^4u}{dt^4}+32\frac{\Delta t^5}{120}\frac{d^5u}{dt^5} + O(\Delta t^6). \end{aligned}\end{split}\]

We now multiply the Taylor series expansions with the corresponding coefficient and group the terms per order of the derivative:

\[\begin{split}\begin{aligned} \left.\frac{du}{dt}\right|_{t^n} = &(a_{-2}+a_{-1}+a_{0}+a_{1}+a_{2})u^{n} + \\ &(-2a_{-2}-a_{-1}+a_{1}+2a_{2})\Delta t\frac{du}{dt} + \\ &(4a_{-2}+a_{-1}+a_{1}+4a_{2})\frac{\Delta t^2}{2}\frac{d^2u}{dt^2} + \\ &(-8a_{-2}-a_{-1}+a_{1}+8a_{2})\frac{\Delta t^3}{6}\frac{d^3u}{dt^3} + \\ &(16a_{-2}+a_{-1}+a_{1}+16a_{2})\frac{\Delta t^4}{24}\frac{d^4u}{dt^4} + \\ &(-32a_{-2}-a_{-1}+a_{1}+32a_{2})\frac{\Delta t^5}{120}\frac{d^5u}{dt^5} + O(\Delta t^6). \end{aligned}\end{split}\]

In order for \(\frac{du}{dt}\mid_{t^n}\) to converge to \(du/dt\) when \(\Delta t \to 0\), we must have:

\[\begin{split}\begin{aligned} \mathrm{c1:}& \quad a_{-2}+a_{-1}+a_{0}+a_{1}+a_{2} = 0 \\ \mathrm{c2:}& \quad (-2a_{-2}-a_{-1}+a_{1}+2a_{2})\Delta t = 1, \end{aligned}\end{split}\]

which provides two necessary conditions, there remaining three parameters to choose in order to have the highest accuracy. This implies cancelling the next three truncation errors:

\[\begin{split}\begin{aligned} \mathrm{c3:}& \quad 4a_{-2}+a_{-1}+a_{1}+4a_{2} = 0 \\ \mathrm{c4:}& \quad -8a_{-2}-a_{-1}+a_{1}+8a_{2} = 0 \\ \mathrm{c5:}& \quad 16a_{-2}+a_{-1}+a_{1}+16a_{2} = 0. \end{aligned}\end{split}\]

Conditions c1 to c5 provide five equations for five unknowns whose solution is:

(3.18)\[a_{-2}=\frac{1}{12\Delta t}, \quad a_{-1}=-\frac{8}{12\Delta t}, \quad a_{0}=0, \quad a_{1}=\frac{8}{12\Delta t}, \quad a_{2}=-\frac{1}{12\Delta t}.\]

Our higher order approximation for the first derivative is therefore

(3.19)\[\left.\frac{du}{dt}\right|_{t^n} \approx \frac{u^{n-2}-8u^{n-1}+8u^{n+1}-u^{n+2}}{12\Delta t}. \]

The leading term of the truncation error is

\[(-32a_{-2}-a_{-1}+a_{1}+32a_{2})\frac{\Delta t^5}{120}\frac{d^5u}{dt^5},\]

which, after substituting the values of the coefficients (3.18), is

\[-\frac{\Delta t^4}{30}\frac{d^5u}{dt^5}.\]

Our approximation (3.19) is, therefore, a 4th order approximation to the first derivative.

The method can be generalized to obtain the \(p^{th}\) order approximation of the derivative using the functions values \(u^{n-m},\dotsc,u^{n+m}\):

(3.20)\[\left.\frac{du}{dt}\right|_{t^n} \approx a_{-m}u^{n-m}+\dotsb+a_{0}u^{n}+\dotsb+a_{m}u^{n+m}, \]

To build the system of equations whose solution provides the unknown coefficients \(a_{n-m},\dotsc,a_{n+m}\), we use the Taylor series expansion for each term \(u^{n+q}, \quad q=-m,\dotsc,m\):

\[u^{n+q} = u^n + q\Delta t\frac{du}{dt}+q^2\frac{\Delta t^2}{2}\frac{d^2u}{dt^2}+\dotsb+q^p\frac{\Delta t^p}{p!}\frac{d^pu}{dt^p}+O(\Delta t^{p+1})\]

in (3.20) and group the terms according to the order of the derivative in which they appear. Then, we require that:

1. The sum of coefficients \(a_q\) multiplying a derivative of order \(k<p\) be zero;

2. The sum of coefficients \(a_q\) multiplying the derivative of order \(p\) be one.

We thus obtain a system of \(p+1\) equations for the \(2m+1\) coefficients \(a_q\). Requirements 1 and 2 can only be satisfied if there are \(2m+1>p+1\) points, i.e., we must have \(2m>p\).

If there are more points than needed, we used them to cancel the next few terms in the truncation error. We can use \(2m+1\) points to cancel up to order \(2m-p+1\).

3.4.3. Evaluating the truncation error for 1st derivative formulas

To evaluate the effect of the truncation error, we consider the following sinusoidal function

\[u(t)=U\sin\left( 2\pi\frac{t}{T} \right) = U\sin(\omega t), \quad \omega=\frac{2\pi}{T},\]

whose first derivative is \(U\omega \cos(\omega t)\). In Fig. 3.3, the error of the first derivative is shown for the forward, backward, centred and 4th order difference formulas.

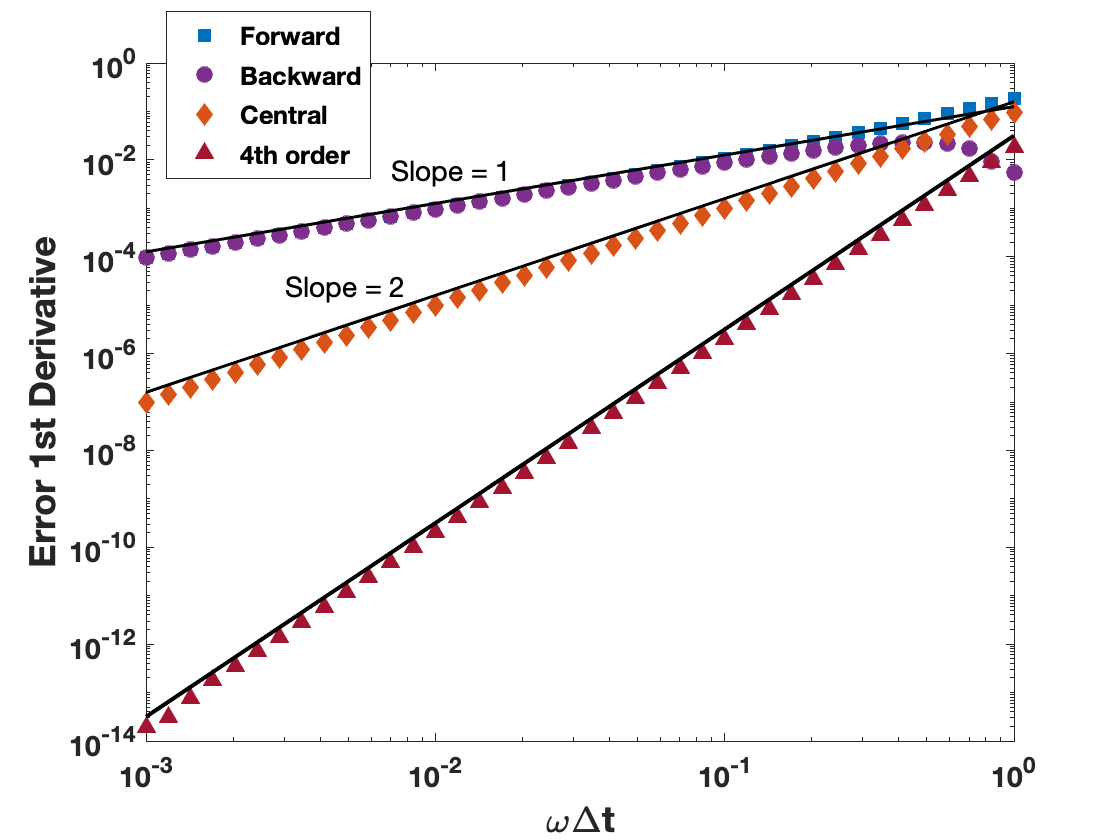
Fig. 3.3 Error of the first derivative formulas.

As \(\omega \Delta t \to 0\), the error of the 4th order formula decreases much faster than those of the centred (2nd order) and forward/backward (1st order) formulas.