3.1. Algebraic approximation of the first derivative

Let us consider a function \(u(t)\) that depends continuously on \(t\).

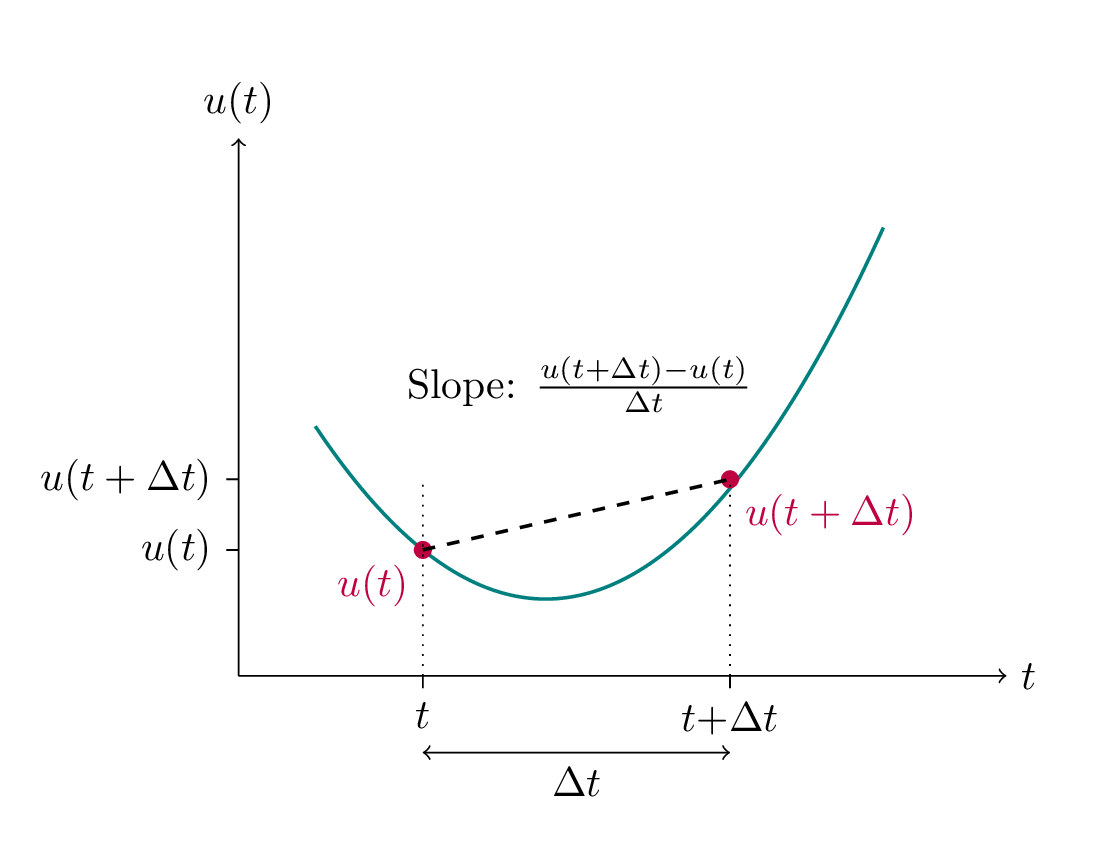
Fig. 3.1 A continuous function \(u(t)\). Two points \(t\) and \(t+\Delta t\) are indicated alont the horizontal axis, and their functional values are indicated on the vertical axis. The slope between the two points is an approximation for the derivative at the point \(t\).

The slope between the two point \(t\) and \(t+\Delta t\) is an approximation of the derivative of \(u(t)\) in the point \(t\). The distance between \(t\) and \(\Delta t\) determines how good the approximation is. If we reducing the time step \(\Delta t\), i.e., shift the rightmost point closer to the point \(t\), we get an improved approximation for the derivatice. The exact derivative, is found by letting \(\Delta t\) approah zero:

(3.1)\[\frac{du}{dt} = \lim_{\Delta t \to 0} \frac{u(t+\Delta t)-u(t)}{\Delta t}.\]

We can obtain an algebraic approximation to \(du/dt\) simply by relaxing the requirement that \(\Delta t \to 0\), which means that we allow \(\Delta t\) to be a finite, small non-zero number:

(3.2)\[\frac{du}{dt} \approx \frac{u(t+\Delta t)-u(t)}{\Delta t}.\]

If instead of a continuous \(t\), we use discrete values \(t^n=n\Delta t\), we can write the algebraic approximationin Eq. (3.2) as:

(3.3)\[\frac{du}{dt} \approx \frac{u^{n+1}-u^n}{\Delta t},\]

where \(u^{n+1}=u(t^{n+1})=u(t^n+\Delta t)\) and \(u^{n}=u(t^n)\).

When dropping the requirement \(\Delta t \to 0\) to obtain the algebraic approximation, we are introducing errors in the calculation of \(du/dt\). We must now find out how large can these errors be.