6.2. The Implicit Scheme

We can derive a general implict scheme by noting that the Crank-Nicholson scheme has the spatial derivatives at \(t^n\) and \(t^{n+1}\) multiplied by \(1/2\). We can generalize the formula in the following fashion:

(6.6)\[ \frac{u_m^{n+1}-u_m^n}{\Delta t} = -\frac{c}{2}\left(\alpha\frac{u_{m+1}^{n+1}-u_{m-1}^{n+1}}{2\Delta x} + (1-\alpha)\frac{u_{m+1}^{n}-u_{m-1}^{n}}{2\Delta x}\right)\]

The value of \(\alpha\) determines the nature of the scheme:

\[\begin{split}\begin{aligned} \alpha &= 0 \quad \text{Fully explicit scheme} \\ \alpha &= 0.5 \quad \text{Crank-Nicholson scheme} \\ \alpha &= 1 \quad \text{Fully implicit scheme} \end{aligned}\end{split}\]

6.2.1. Consistency, stability and convergence

The formula of the amplification factor (6.7) can be generalized following (6.6):

(6.7)\[ G = \frac{u_{m}^{n+1}}{u_{m}^{n}} = \frac{1-(1-\alpha)(\sigma/2)i\sin\lambda \Delta x}{1+\alpha(\sigma/2)i\sin\lambda \Delta x},\]

The effect of varying \(\alpha\) in the stability is shown below:

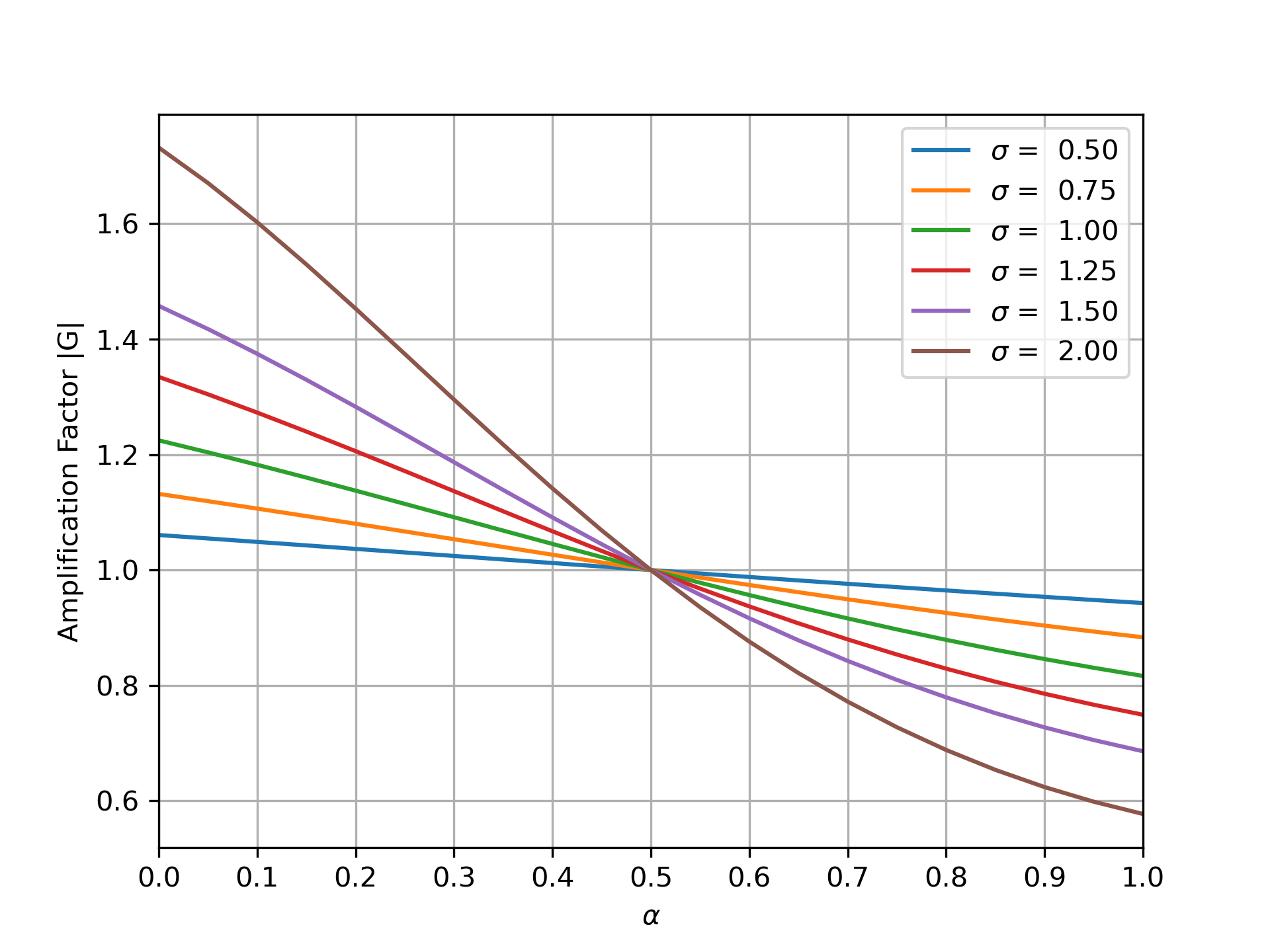
Fig. 6.1 The amplification factor of the general implicit scheme, for a range of CFL numbers and \(\alpha\).

The implicit scheme \(\alpha > 0.5\) is damping and for \(\alpha < 0.5\), the scheme is unconditionally unstable. The damping effect of the numerical diffusion of the implicit scheme increases as the CFL number increases.

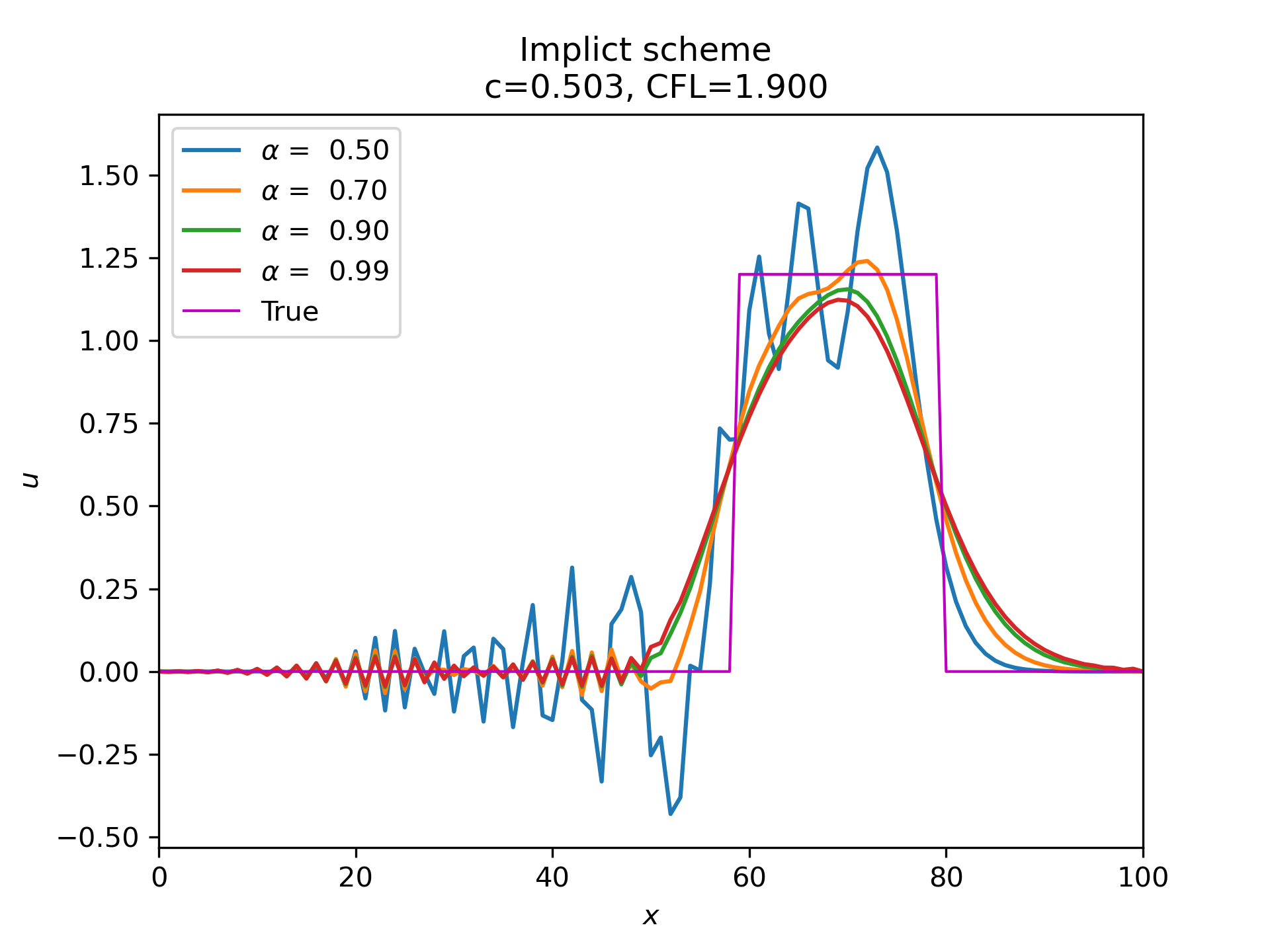
Fig. 6.2 The solution of the implicit scheme after 10 time steps for a top hat initial condition, for CFL numbers of 1.9 and \(\alpha=0.5, 0.7, 0.9, 0.99\), with \(\Delta t=2\) and \(\Delta x=1\).